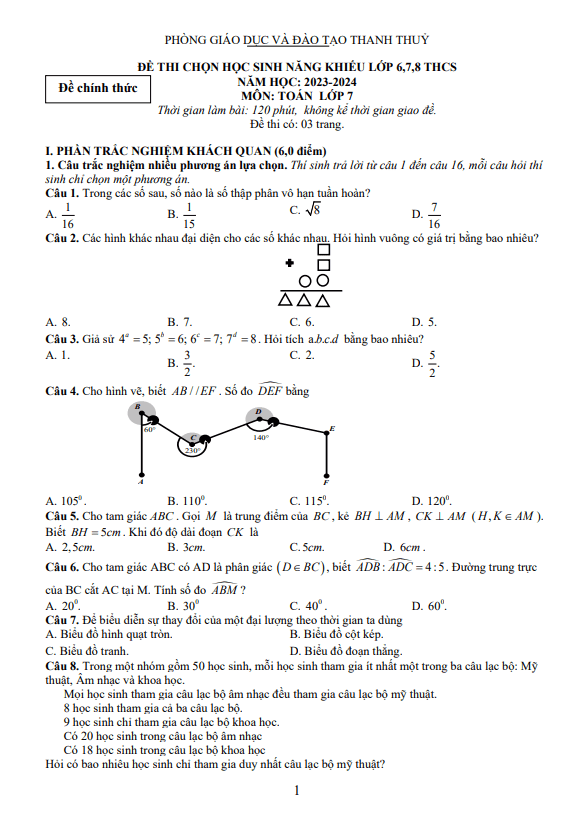
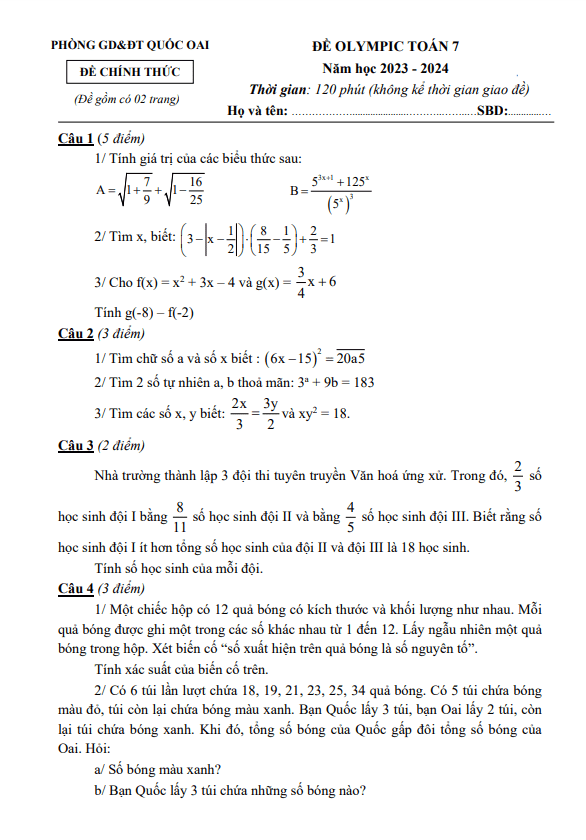THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề học sinh giỏi huyện Toán 7 năm 2016 – 2017 phòng GD&ĐT Kim Thành – Hải Dương; đề thi có đáp án và lời giải chi tiết.
Trích dẫn đề học sinh giỏi huyện Toán 7 năm 2016 – 2017 phòng GD&ĐT Kim Thành – Hải Dương:
+ Cho tam giác ABC có ba góc nhọn (AB < AC). Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi I là giao của CD và BE, K là giao của AB và DC.
a) Chứng minh rằng: ADC = ABE.
b) Gọi M và N lần lượt là trung điểm của CD và BE. Chứng minh rằng AMN đều.
c) Chứng minh rằng IA là phân giác của góc DIE.
+ Chứng minh rằng với n nguyên dương thì 3n+2 – 2n+2 + 3n – 2n chia hết cho 10.
+ Tìm các cặp số nguyên (x;y) thỏa mãn: x + 2y = 3xy + 3.