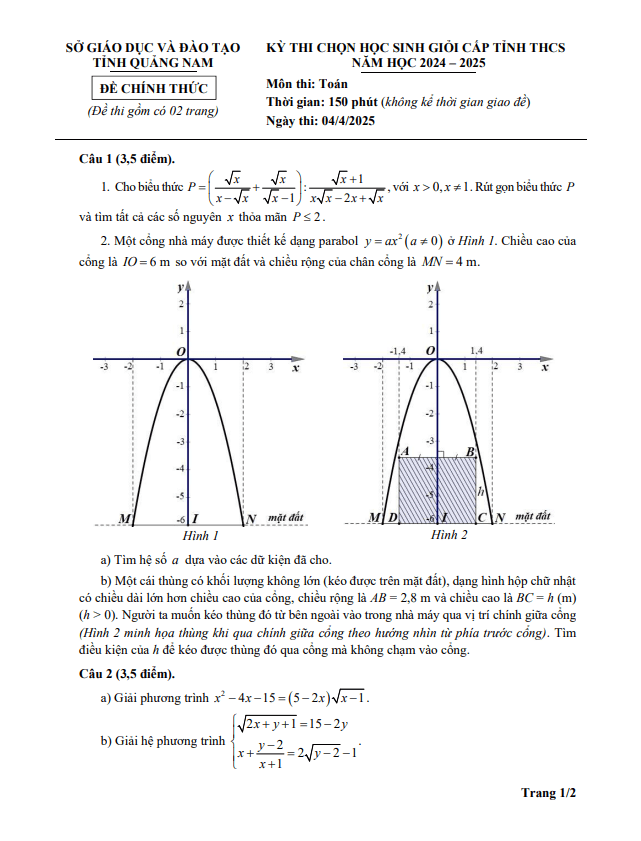
THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề khảo sát học sinh giỏi môn Toán 9 năm học 2024 – 2025 phòng Giáo dục và Đào tạo huyện Kim Thành, tỉnh Hải Dương; kỳ thi được diễn ra vào ngày … tháng 08 năm 2024.
Trích dẫn Đề khảo sát HSG Toán 9 năm 2024 – 2025 phòng GD&ĐT Kim Thành – Hải Dương:
+ Cho p là một số nguyên tố. Tìm p để tổng các ước nguyên dương của p4 là một số chính phương.
+ Cho hình vuông ABCD, có độ dài cạnh bằng a. N là một điểm di chuyển trên AB (N khác A, B). Đường thẳng CN cắt đường thẳng AD tại E, đường thẳng vuông góc với CE tại C cắt đường thẳng AB tại F. a) Chứng minh. b) Tìm vị trí của điểm N trên AB để diện tích tứ giác ACFE gấp 3 lần diện tích hình vuông ABCD.
+ Giả sử mỗi điểm trong mặt phẳng được tô bằng một trong 2 màu đen và trắng. Chứng minh tồn tại một hình chữ nhật có các đỉnh cùng màu.