THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh đề chính thức kỳ thi tuyển sinh vào lớp 10 THPT môn Toán (chuyên) năm học 2025 – 2026 sở Giáo dục và Đào tạo thành phố Hải Phòng. Đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm.
Trích dẫn Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2025 – 2026 sở GD&ĐT Hải Phòng:
+ Gọi S là tập hợp gồm các số tự nhiên có hai chữ số khác nhau, tạo thành từ các chữ số 0, 1, 2, 3, 4, 5 và 6. Mỗi bạn An và Bình viết ngẫu nhiên một số thuộc tập S lên bảng. Tính xác suất để tổng của hai số được viết lên bảng là số chẵn.
+ Lúc 6 giờ sáng, bạn Hải đi xe đạp từ vị trí A đến vị trí B, quãng đường AB dài 25 km. Khi đi được 2/5 quãng đường AB, Hải dừng lại tại vị trí C để ăn sáng 35 phút. Sau đó, Hải tiếp tục đi từ C đến B với tốc độ chậm hơn 2 km/giờ so với tốc độ đi trên đoạn đường AC. Khi đến B, Hải nghỉ lại 45 phút và quay ngược trở lại A (theo tuyến đường ban đầu) với tốc độ bằng 3/4 tốc độ đi đoạn đường từ A đến C. Hải về đến A lúc 10 giờ 20 phút sáng cùng ngày. Hỏi bạn Hải đến B lúc mấy giờ (giả sử tốc độ trên từng đoạn đường là không đổi)?
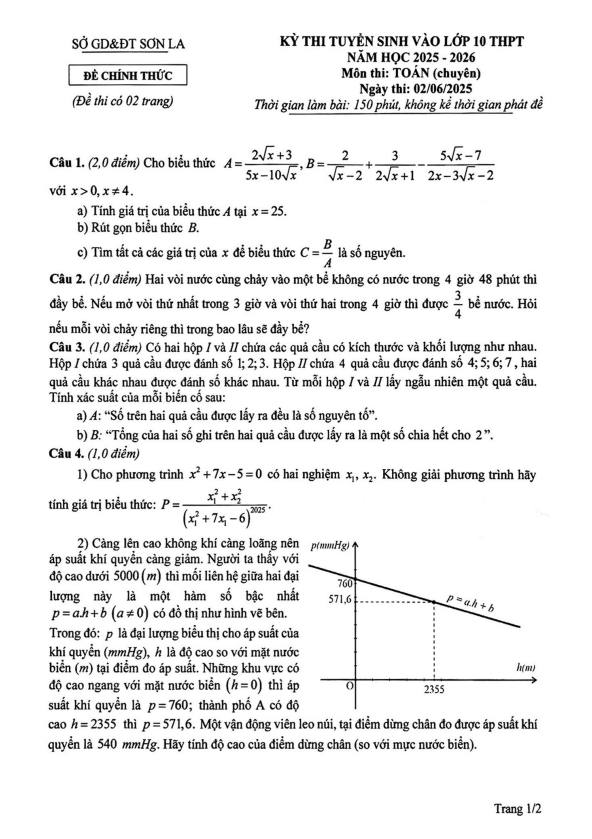
+ Cho tập hợp S = {x ∈ Z | 1 ≤ x ≤ 15}. Xét T là một tập con của S và có tính chất: với a, b, c bất kì thuộc T (a, b, c đôi một khác nhau) thì tích abc không là số chính phương. Hỏi T có nhiều nhất bao nhiêu phần tử? (Tập hợp A được gọi là tập con của tập hợp B nếu mọi phần tử của A đều là phần tử của B).
File WORD (dành cho quý thầy, cô): TẢI XUỐNG