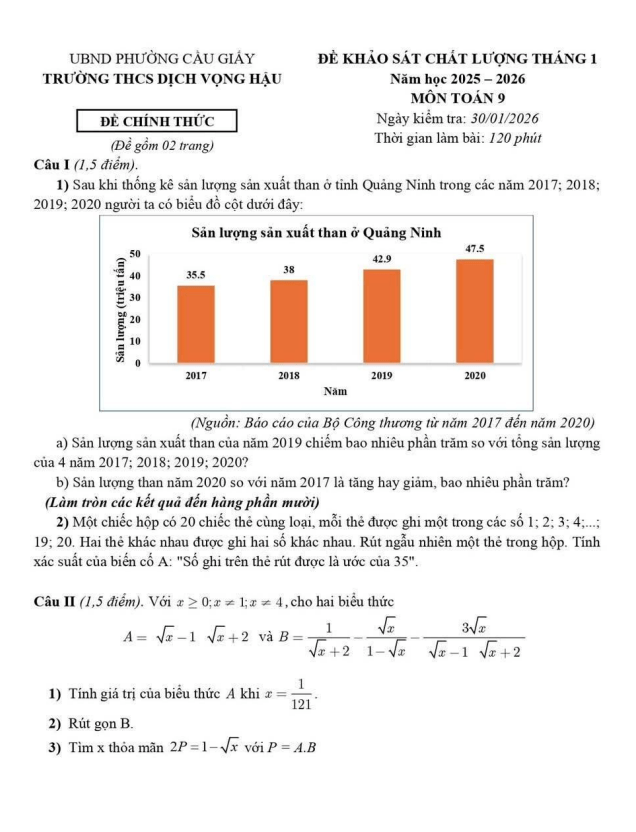
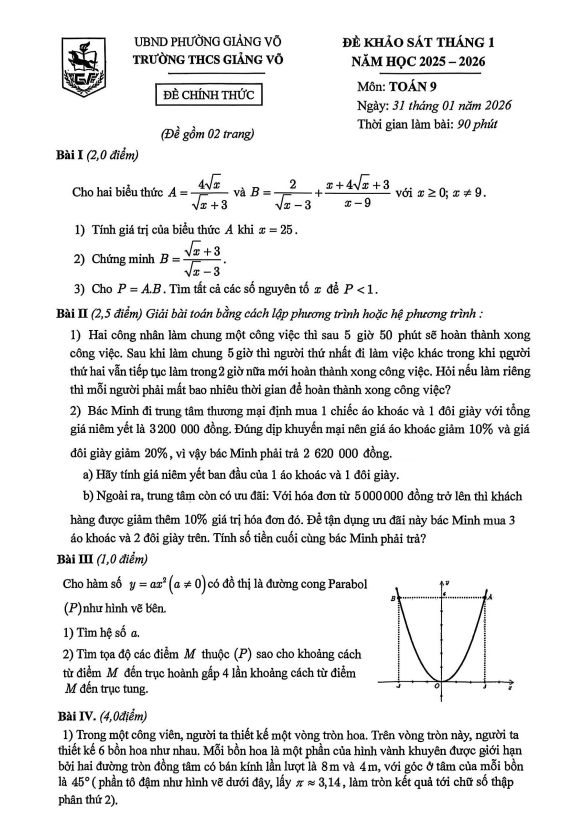
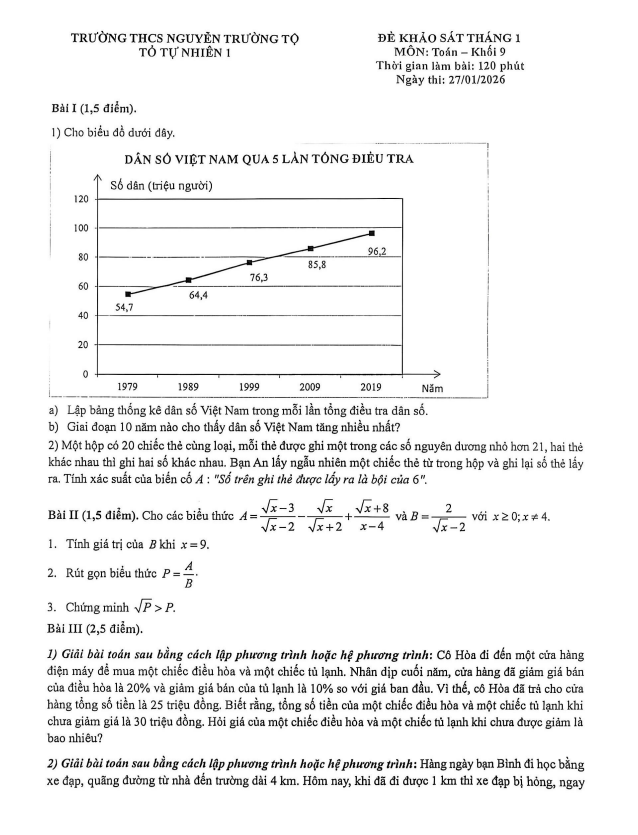
THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh đề khảo sát chất lượng môn Toán 9 tháng 2 năm học 2025 – 2026 trường THCS Bế Văn Đàn, phường Đống Đa, thành phố Hà Nội.
Trích dẫn Đề khảo sát Toán 9 tháng 2 năm 2026 trường THCS Bế Văn Đàn – Hà Nội:
+ Một cây quạt giấy có chiều dài nan quạt 27 cm, độ dài phần nan quạt không dán giấy là 12 cm, biết độ xòe căng nhất của quạt là một góc 150°. Tính diện tích giấy để làm nên chiếc quạt như trên, biết rằng cần hai lớp giấy để dán hai mặt của chiếc quạt đó. (Bỏ qua phần nếp gấp; lấy π ≈ 3,14; kết quả làm tròn đến hàng phần mười của centimet vuông).
+ Cho đường tròn (O) với đường kính AC. Trên đoạn OC lấy điểm B. Gọi M là trung điểm AB, từ M kẻ dây DE vuông góc với AB. Từ B kẻ BF vuông góc với CD (F thuộc CD). a) Chứng minh bốn điểm B, M, D, F cùng thuộc một đường tròn. b) Chứng minh tứ giác ADBE là hình thoi và MF2 = MB.MC. c) Gọi S là giao điểm của BD với MF, tia CS lần lượt cắt AD, DE tại H và K. Chứng minh DA/DH + DB/DS = DE/DK.
+ Hộp kĩ thuật của một ngôi nhà được đặt trong góc tường và chiếm phần diện tích của một hình chữ nhật với kích thước 60cm x 90cm. Để tận dụng không gian, chủ nhà dự định lắp đặt một tấm vách sát với hộp kĩ thuật và các đầu vách chạm vào tường (như hình vẽ) để tạo ra hai khu vực lưu trữ đồ (phần tô đậm). Tính chiều dài của tấm vách để hai khu vực lưu trữ đồ chiếm tổng diện tích nhỏ nhất.